树(tree) 二叉树基础 - Golang
什么是树(Tree)?
如下图就是一棵树:
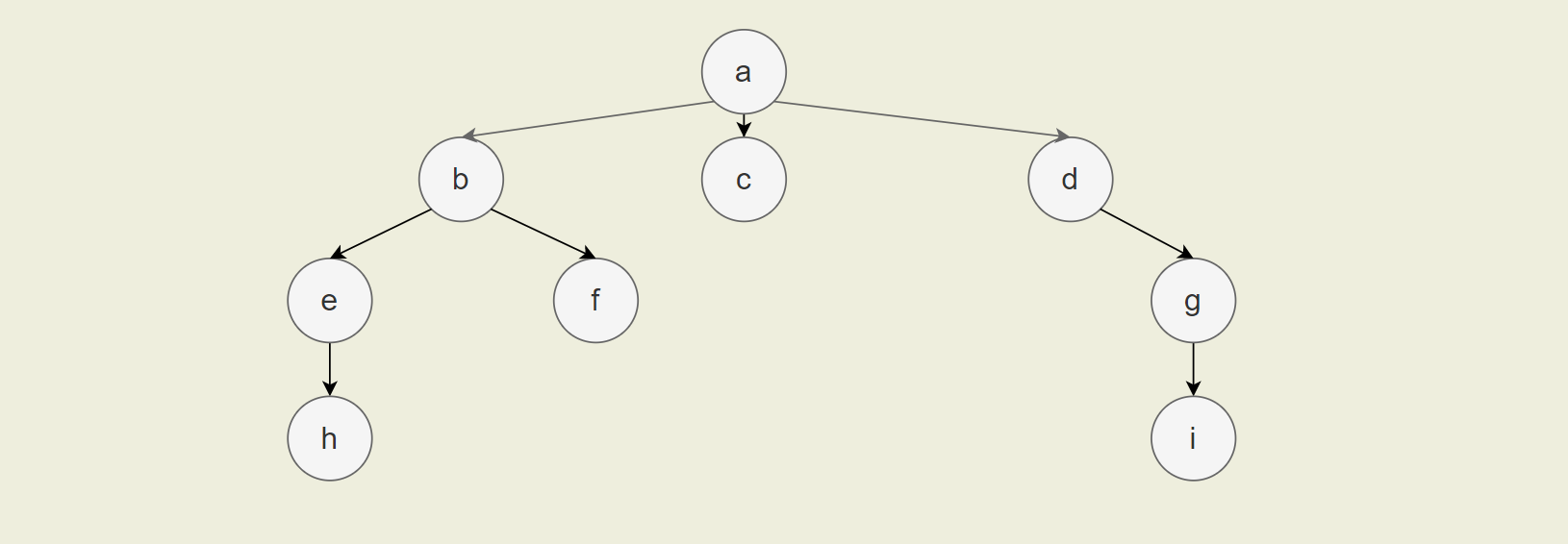
树不同于线性表中的链表、队列、栈,树结构是一种非线性存储结构,存储的是具有“一对多”关系的数据元素的集合。它具有以下的特点:
树的术语
节点的度 :一个节点含有的子树的个数称为该节点的度;
树的度 :一棵树中,最大的节点度称为树的度;
叶节点或终端节点 :度为零的节点;
非终端节点或分支节点 :度不为零的节点;
父亲节点或父节点 :若一个节点含有子节点,则这个节点称为其子节点的父节点;
孩子节点或子节点 :一个节点含有的子树的根节点称为该节点的子节点;
兄弟节点 :具有相同父节点的节点互称为兄弟节点;
节点的层次 :从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
树的高度或深度 :树中节点的最大层次;
堂兄弟节点 :父节点在同一层的节点互为堂兄弟;
节点的祖先 :从根到该节点所经分支上的所有节点;
子孙 :以某节点为根的子树中任一节点都称为该节点的子孙。
森林 :由m(m>=0)棵互不相交的树的集合称为森林;
二叉树的性质
经过前人的总结,二叉树具有以下几个性质:
二叉树中,第 i 层最多有 个节点。
如果二叉树的深度为 K,那么此二叉树最多有 个节点。
二叉树中,终端节点数(叶子节点数)为 ,度为 2 的节点数为 ,则 。
下面证明第三点:
假设二叉树有N个节点,那么N = + +
从树的叶子节点到根节点思考,那么二叉树的边(两个节点的连接线)B = N - 1(除了根节点每个节点都有一条边)
从根节点到叶子节点思考,度为2的节点有两条变、度为1的节点有一条边、度为0的节点是叶子节点没有边,得到 B = 0* + 1* + 2*
因此我们得到 N - 1 = + 2*
使用 + + 替换N,得到 + + - 1 = + 2*
得到
二叉树的存储结构
顺序存储
指的是使用顺序表(数组)存储二叉树。需要注意的是,顺序存储只适用于完全二叉树。换句话说,只有完全二叉树才可以使用顺序表存储。因此,如果我们想顺序存储普通二叉树,需要提前将普通二叉树转化为完全二叉树
链式存储
二叉树并不适合用数组存储,因为并不是每个二叉树都是完全二叉树,普通二叉树使用顺序表存储或多或多会存在空间浪费的现象
二叉树的数组表示
为了方便描述一个二叉树,我们使用数组表示,如果是普通二叉树我们先转化成完全二叉树,为空的节点可以约定一个值(比如NULL)来表示,我们从树的根节点开始按从底层到高层从左到右的顺序依次排列节点。
示例:
5
/ \
9 20
/ \
15 7
/
10
转化成完全二叉树后:
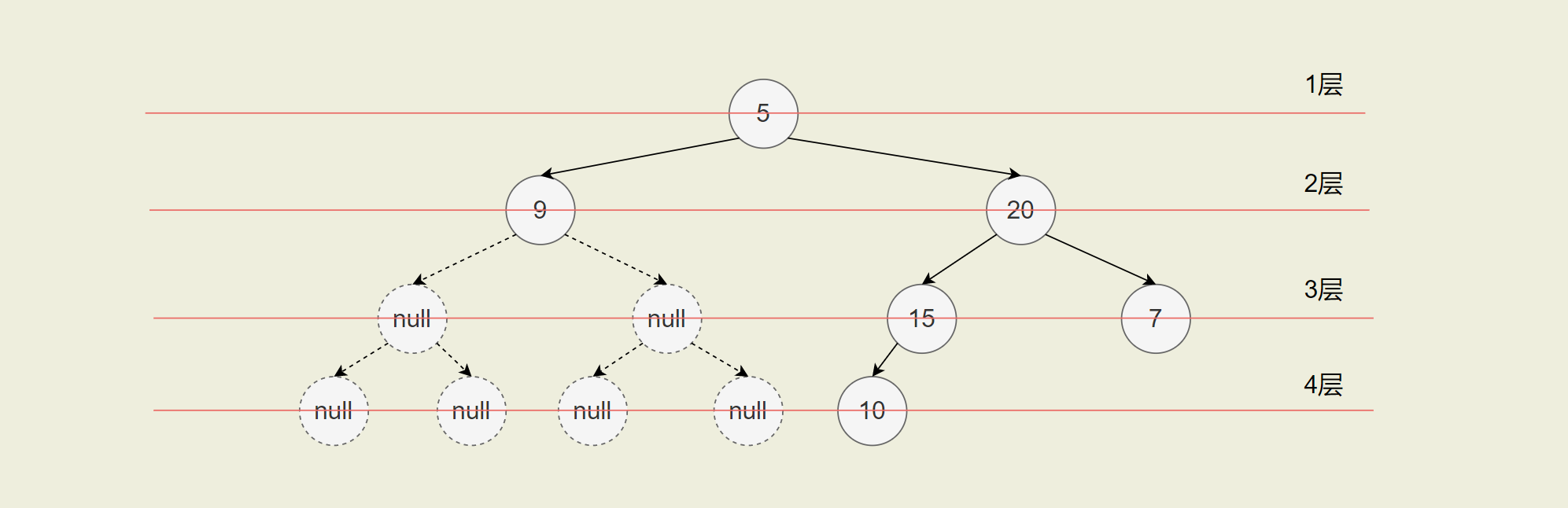
最终得到数组: [5,9,20,null,null,15,7,null,null,null,null,10]
假设某个节点索引值为index(根节点为0),那么节点索引之间满足以下算式:
左子节点索引: 2*index+1
右子节点索引为: 2*index+2
父节点索引为: (index-1)/2
基于以上的数组表示法,我们构造一个函数BuildTree ,输入数组得到一棵二叉树并返回根节点,使用0表示空节点:
tree.go
package tree
type Node struct {
Val int
Left, Right *Node
}
// BuildTree 输入一个切片 :[3,9,20,0,0,15,7]
func BuildTree(l []int) (root *Node) {
length := len(l)
if length == 0 {
return root
}
var nodes = make([]*Node, length)
root = &Node{
Val: l[0],
}
nodes[0] = root
//循环输入的数组切片,依次判断每一个节点的左右节点是否存在并创建
for i := 0; i < length; i++ {
currentNode := nodes[i]
if currentNode == nil {
continue
}
leftIndex := 2*i + 1
if leftIndex < length && l[leftIndex] != 0 {
currentNode.Left = &Node{
Val: l[leftIndex],
}
nodes[leftIndex] = currentNode.Left
}
rightIndex := 2*i + 2
if rightIndex < length && l[rightIndex] != 0 {
currentNode.Right = &Node{
Val: l[rightIndex],
}
nodes[rightIndex] = currentNode.Right
}
}
return root
}
这样创建一棵二叉树:
root := tree.BuildTree([]int{3, 9, 20, 0, 0, 15, 7})
树转化成数组
上面我们使用BuildTree函数从数组创建了一棵树,那么我们下面再写一个函数ConvertToArr做一个逆运算将一棵树转化成数组来表示,先看代码:
// ConvertToArr 树转化成数组
func ConvertToArr(root *Node) []int {
if root == nil {
return []int{}
}
result := indexRecursion(root, 1, 0, []int{})
// 删除末尾的0
for i := len(result) - 1; i >= 0; i-- {
if result[i] == 0 {
result = result[:i]
} else {
break
}
}
return result
}
// 索引循环
func indexRecursion(node *Node, level int, index int, result []int) []int {
//深度为level的树最多有2^level-1个节点,容量不够时扩容依据
if len(result) < (1<<level - 1) {
newArr := make([]int, 1<<level-1)
copy(newArr, result)
result = newArr
}
result[index] = node.Val
if node.Left != nil {
result = indexRecursion(node.Left, level+1, 2*index+1, result)
}
if node.Right != nil {
result = indexRecursion(node.Right, level+1, 2*index+2, result)
}
return result
}
尝试转化一棵树:
root := tree.BuildTree([]int{5, 9, 20, 0, 22, 15, 7, 0, 0, 0, 0, 10, 30})
result := tree.ConvertToArr(root)
fmt.Println(result)
输出:
[5 9 20 0 22 15 7 0 0 0 0 10 30]
上面代码中level表示层次,然后索引从0开始,所以根节点的level=1,index=0 ConvertToArr函数是对二叉树的性质及二叉树数组索引算式的应用。
如何获取二叉树最大深度?
回忆下概念: 树的深度指的是树中最大的节点层。
这是一道力扣算法题 104.二叉树的最大深度
对于二叉树:
1
/ \
2 3
/ / \
4 5 6
下面给出两种计算方式:
深度优先搜索(DFS)
访问的顺序是:1->2->4->3->5->6
dfsRecursion函数返回的切片是一个按层来排列节点的二维切片,例: [1,[2,3],[4,5,6]]
// MaxDepth 计算树的深度
func MaxDepth(root *Node) int {
return len(dfsRecursion(root, 0, [][]int{}))
}
// 深度优先
func dfsRecursion(node *Node, level int, nodes [][]int) [][]int {
if node == nil {
return nodes
}
// 判断切片长度是否满足要求
if level < len(nodes) {
nodes[level] = append(nodes[level], node.Val)
} else {
nodes = append(nodes, []int{node.Val})
}
nodes = dfsRecursion(node.Left, level+1, nodes)
nodes = dfsRecursion(node.Right, level+1, nodes)
return nodes
}
宽度优先搜索(BFS)
宽度优先就是从上到下,先把每一层遍历完之后再遍历一下一层。
访问的顺序是:1->2->3->4->5->6
我们使用 container/list 来模拟一个Queue,将root节点初始化进队列,然后依次插入节点到头部, 从尾部消耗节点的方式来完成BFS。
代码如下:
func BFS(root *Node) (result [][]int) {
if root == nil {
return result
}
queue := list.New()
queue.PushFront(root)
for queue.Len() > 0 {
var currentLevel []int
listLength := queue.Len()
for i := 0; i < listLength; i++ {
node := queue.Remove(queue.Back()).(*Node)
currentLevel = append(currentLevel, node.Val)
if node.Left != nil {
queue.PushFront(node.Left)
}
if node.Right != nil {
queue.PushFront(node.Right)
}
}
result = append(result, currentLevel)
}
return result
}
References
https://leetcode.cn/problems/maximum-depth-of-binary-tree/
19 November 2023

