B树的定义
B树是一颗多路平衡查找树。我们描述一颗B树时需要指定它的阶数 M ,阶数 M 代表一个树节点最多有多少个查找路径,M=M路,当M=2则是2叉树,M=3则是3叉。
一棵M阶B树,有如下特性:
- 若根节点不是叶子结点,则至少有两棵树。
- 每一个节点最多M棵子树,最多有
M-1个关键字(键值对)。 - 除根节点外,其他的每个分支至少有
ceil(M/2)个子树,至少含有ceil(M/2)-1个关键字。 - 每个节点中的关键字都按照大小顺序排列,每个关键字的左子树的所有关键字都小于它,每个关键字的右子树都大于它。
- 所有叶子节点都位于同一层,或者说根节点到每个叶子节点的长度都相同。
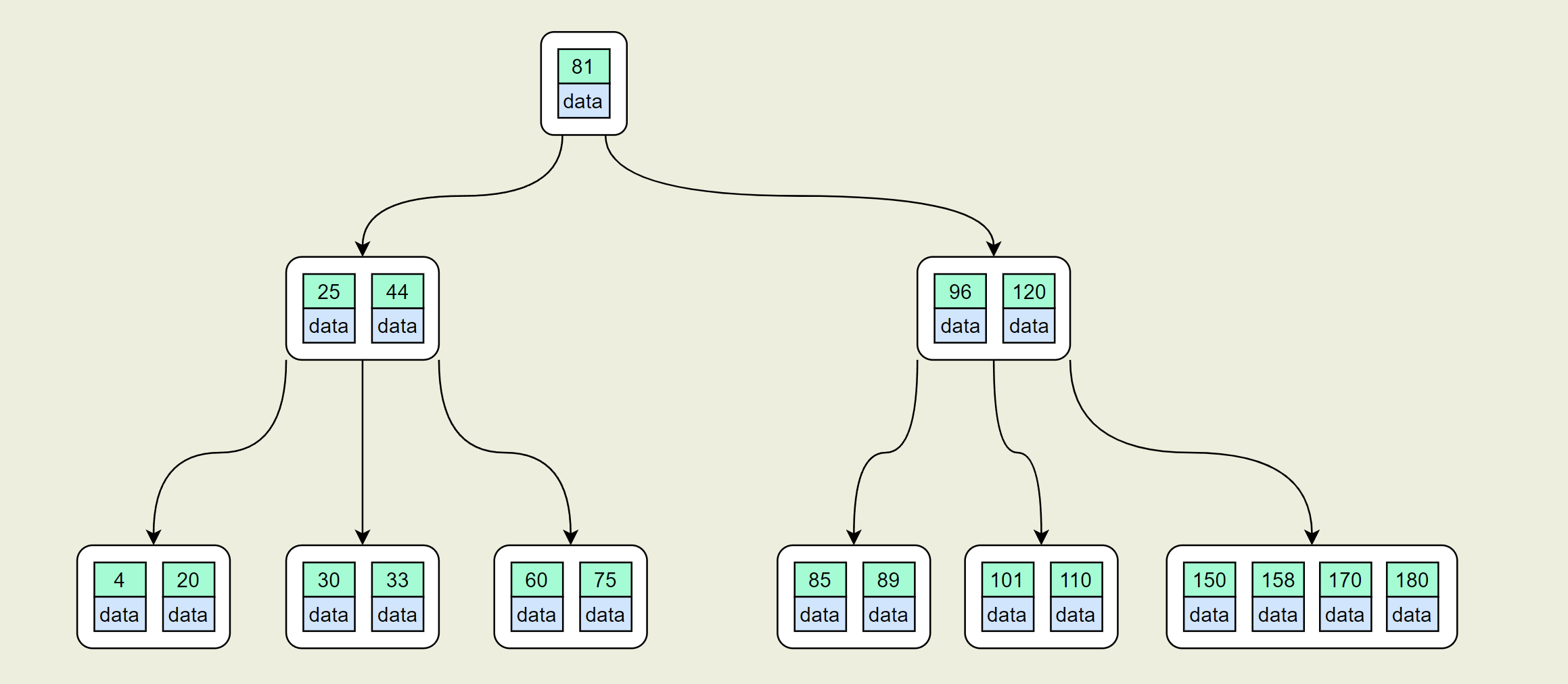
上图是一棵5阶B树。实际B树常用在数据库和文件系统中,为了减少定位记录时所经历的中间过程(树的高度),实际的阶数M都非常大,所以即使存储大量的数据,B树的高度仍然比较小。
B树相对平衡二叉树在节点空间的利用率上进行改进,B树在每个节点保存更多的数据,减少了树的高度,从而提升了查找的性能,在数据库应用中,B树的每个节点存储的数据量大约为4K, 这是因为考虑到磁盘数据存储是采用块的形式存储的,每个块的大小为4K,每次对磁盘进行IO数据读取时,同一个磁盘块的数据会被一次性读取出来,所以每一次磁盘IO都可以读取到B树中一个节点的全部数据。
每个结点中存储了关键字(key)和关键字对应的数据(data),以及孩子结点的指针。在数据库中B树(和B+树)作为索引结构,可以加快查询速度,此时B树中的key就表示键,而data表示了这个键对应的条目在硬盘上的逻辑地址。
B树的插入操作
B树设计初衷就是为了查找,所以查找是最简单的,相反插入、删除反而异常繁琐,每次操作都会多次使用查找。 插入操作,一般搜索树而言,插入就是找到相应的位置,直接加入节点,B树为了数据能够快速被查找,在插入的时候不仅要插入到相应的位置,还需要根据情况来调整树的高度以及宽度,尽可能使树高度下降。
插入操作是指插入一条记录,即(key, value)的键值对。如果B树中已存在需要插入的键值对,则用需要插入的value替换旧的value。若B树不存在这个key,则一定是在叶子结点中进行插入操作。
- 根据要插入的key的值,找到叶子结点并插入。
- 判断当前结点key的个数是否小于等于
M-1,若满足则结束,否则进行第3步。 - 以结点中间的key为中心分裂成左右两部分,然后将这个中间的key插入到父结点中,这个key的左子树指向分裂后的左半部分,这个key的右子支指向分裂后的右半部分,然后将当前结点指向父结点,继续进行第3步。
下面以5阶B树为例,执行插入操作。在5阶B树中,结点最多有4个key,最少有2个key。
- 在空树中插入4

此时根结点就一个key,根结点也是叶子结点
- 插入:20,44,89,96

插入96后此节点超过了最大允许的关键字个数4,此时需要以44为中心进行分裂,新的根节点中包含44这个key
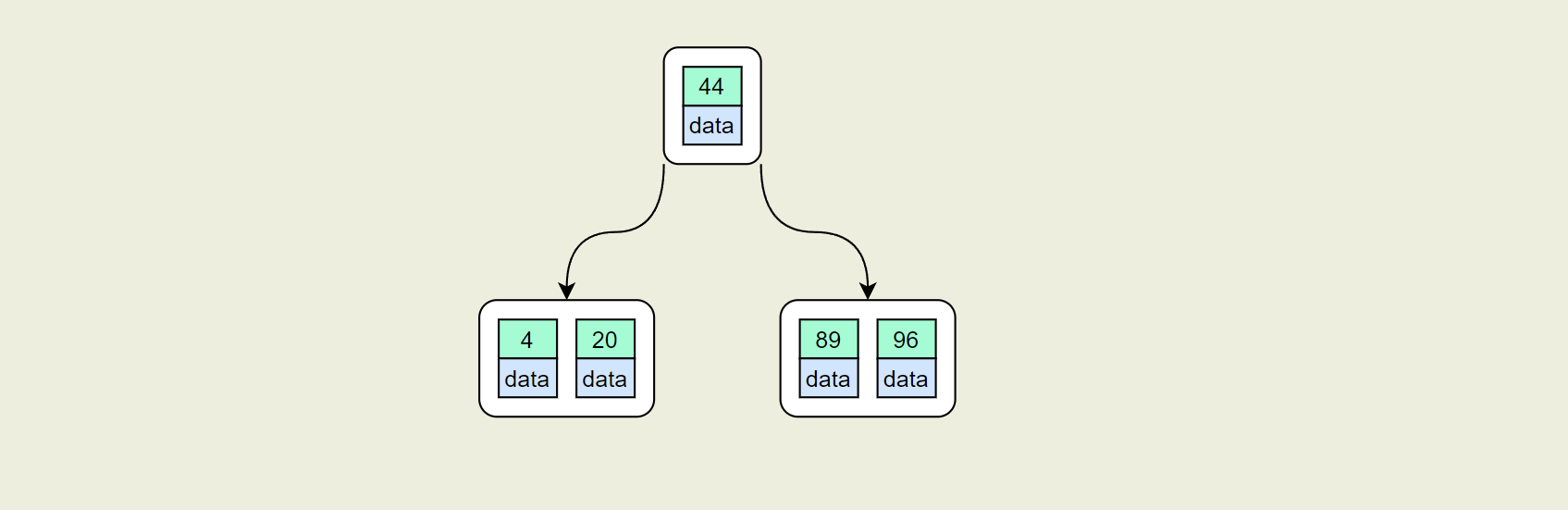
- 插入:25,30,33
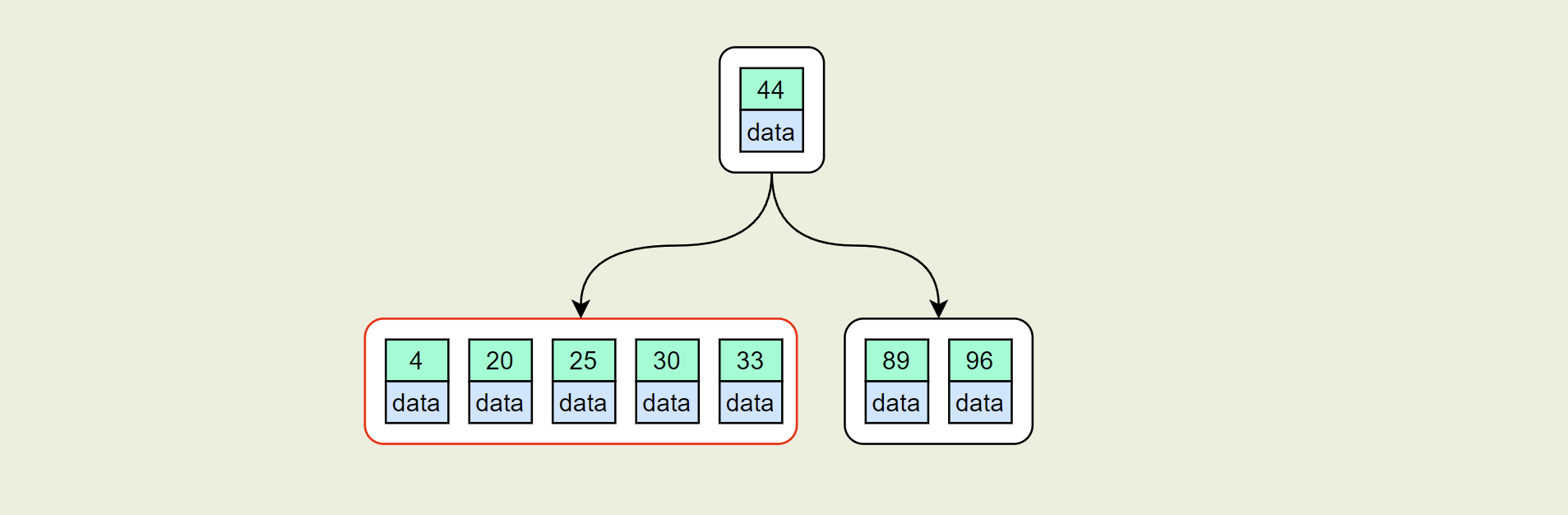
此时左侧节点关键字个数大于4,同样进行分裂操作,得到下图
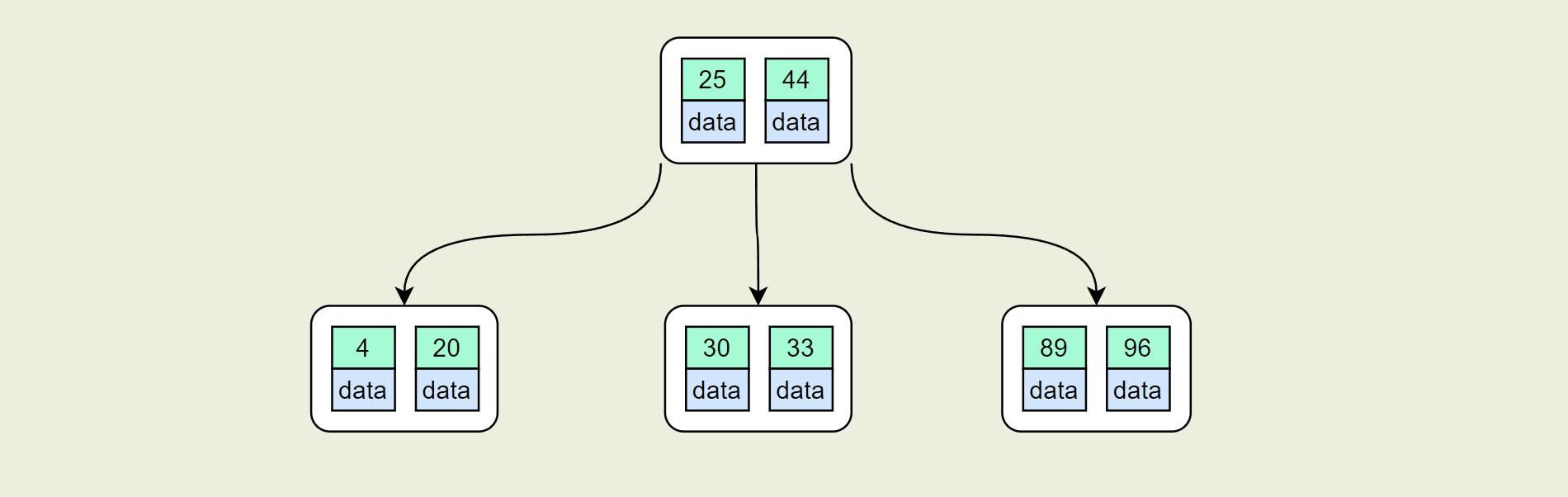
25这个中间key合并到父节点中,左右两侧的key分裂到两个节点中并作为根节点的两个子节点存在
- 插入:60,75,81
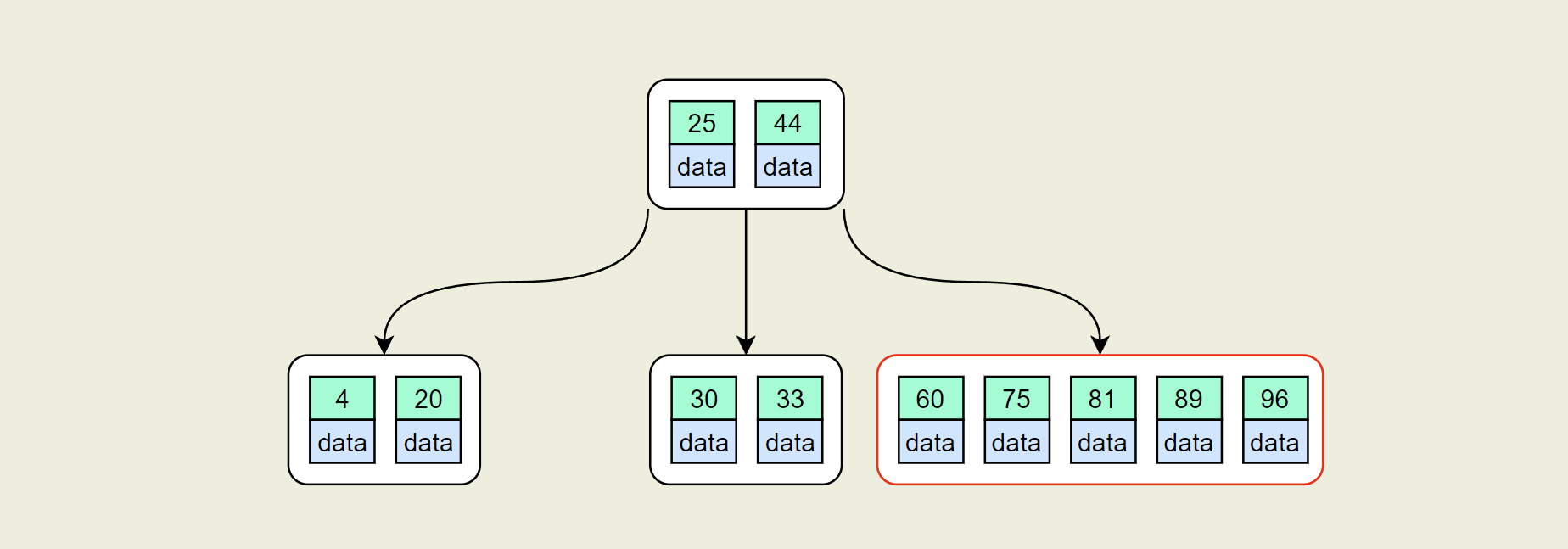
此时最右侧节点关键字个数大于4,同样进行分裂操作,得到下图
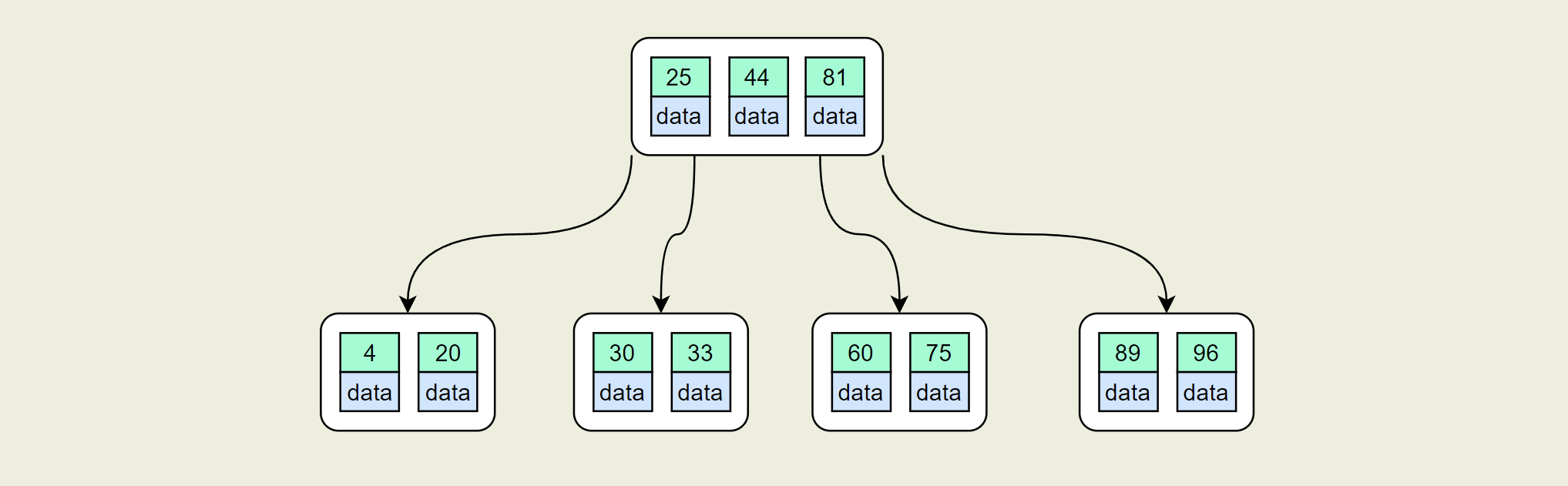
- 插入:85,110,120
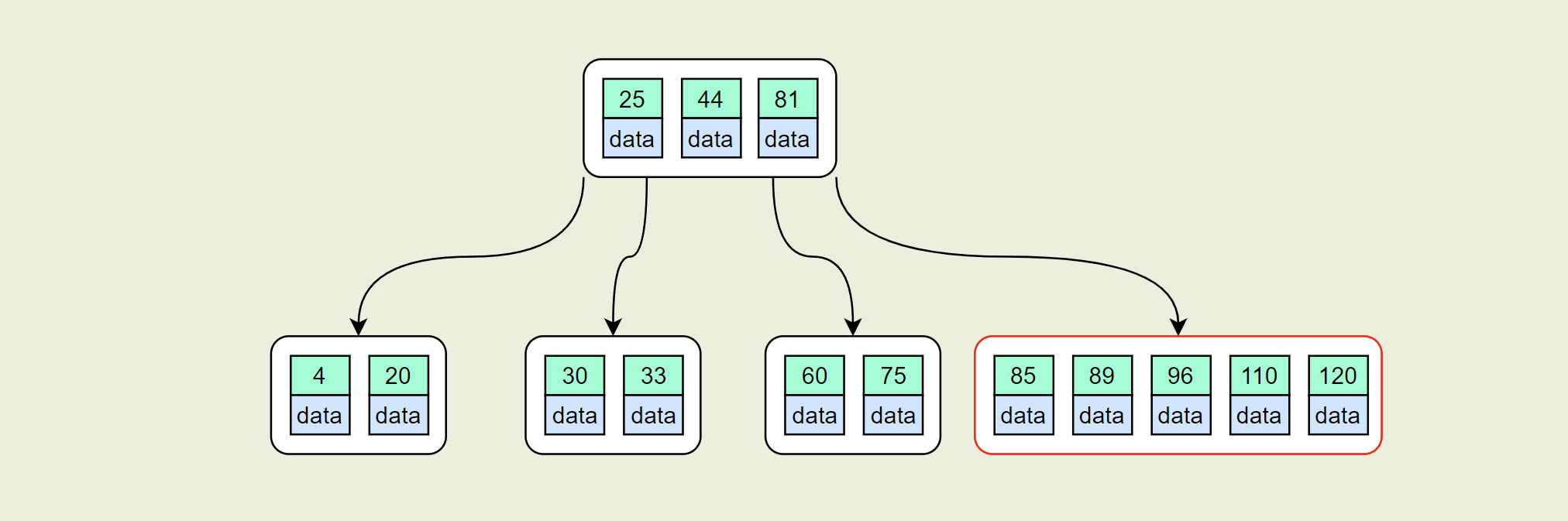
同样进行分裂操作,得到下图
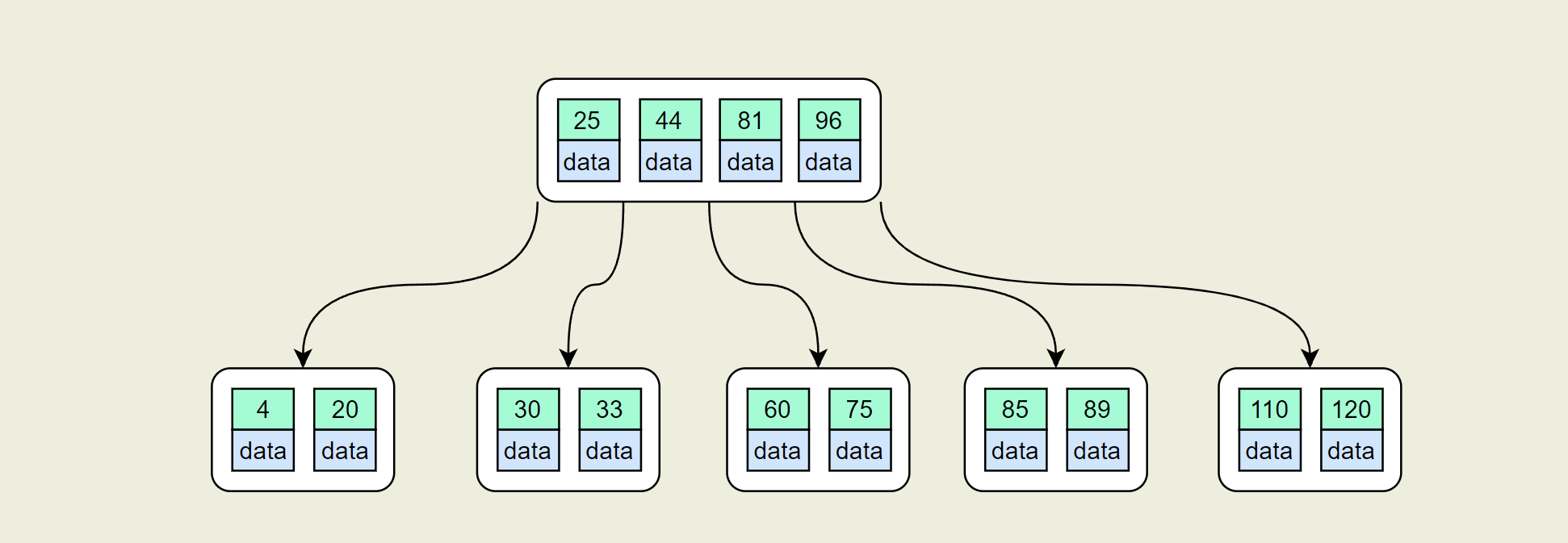
- 插入:101,150,158
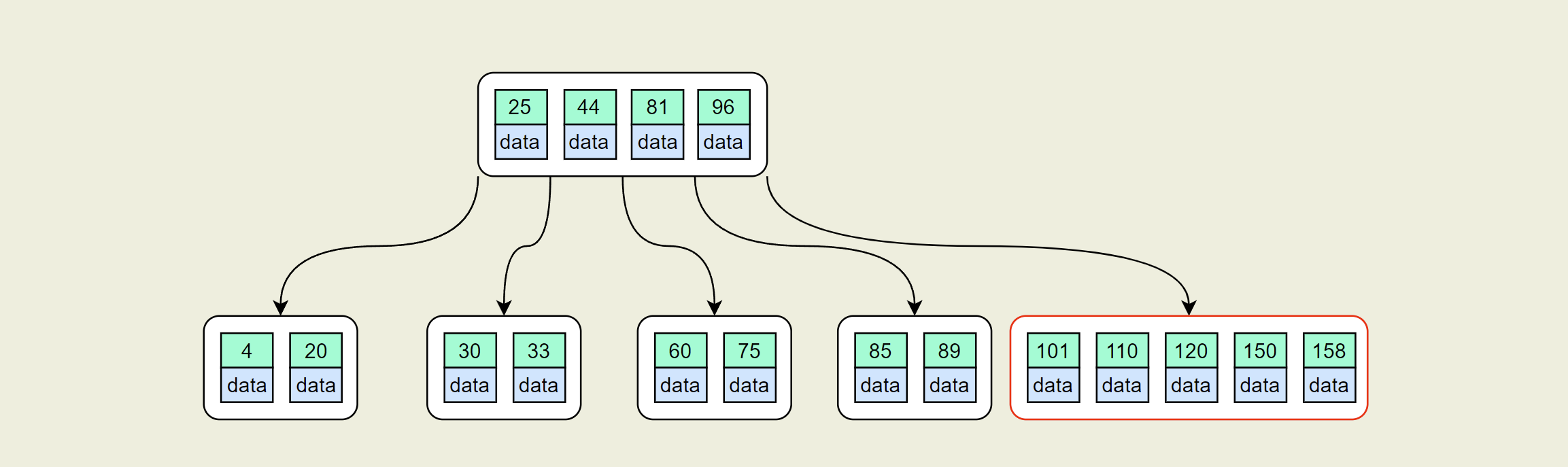
同样进行分裂操作,得到下图
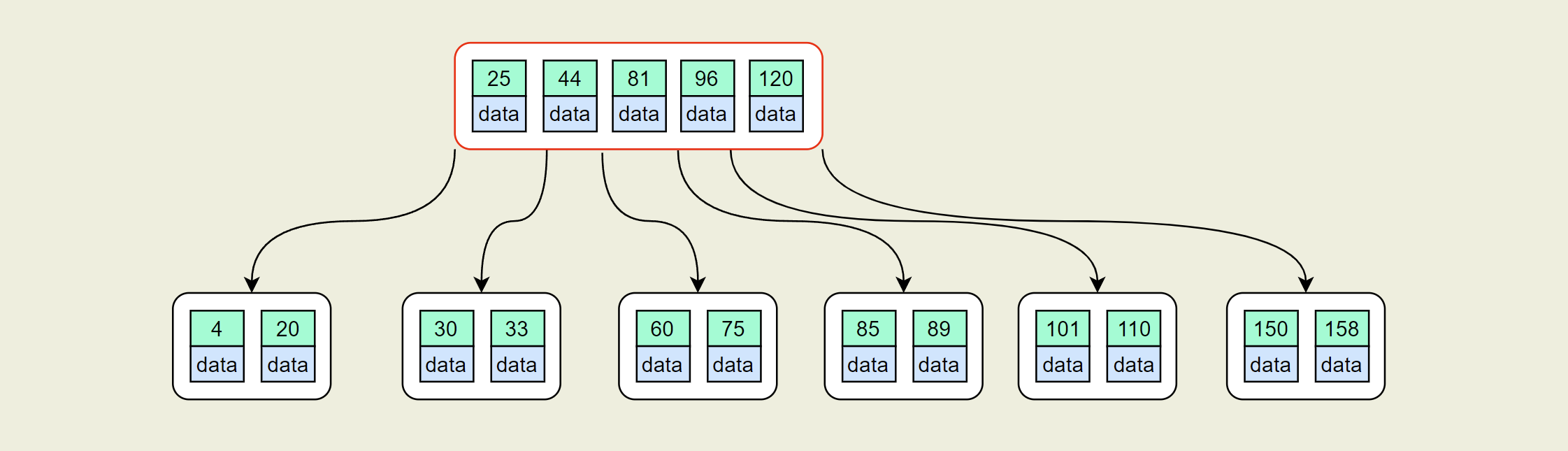
我们发现此时父节点关键字个数大于4,需要对根节点执行分裂操作,根节点的分裂必然导致树的高度增加,这也是B树增加高度的唯一方法,最终得到下图
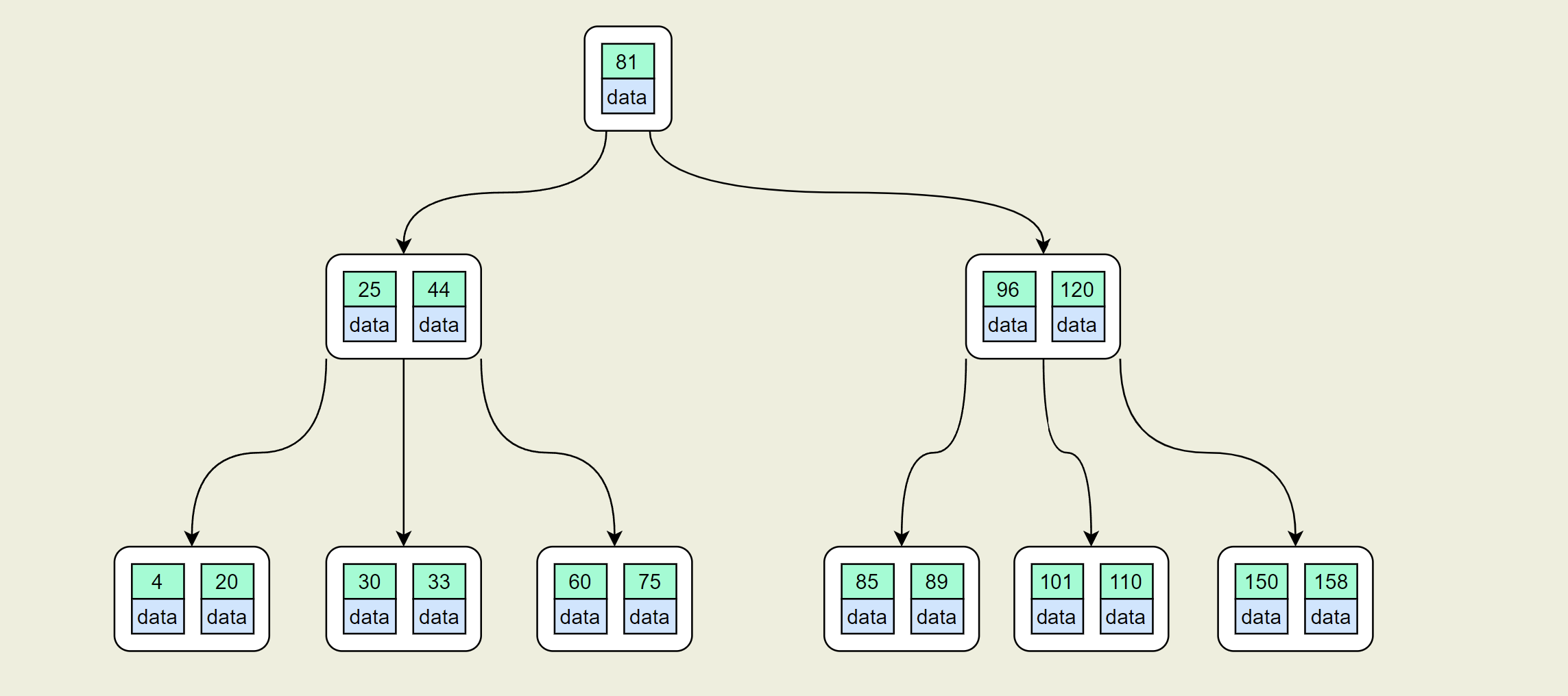
在实现B树的代码中,为了使代码编写更加容易,我们可以将结点中存储记录的数组长度定义为M而非M-1,这样方便底层的结点由于分裂向上层插入一个记录时(中间状态),上层有多余的位置存储这个记录。同时,每个结点还可以存储它的父结点的引用,这样就不必编写递归程序。
一般来说,对于确定的M和确定类型的记录,结点大小是固定的,无论它实际存储了多少个记录。但是分配固定结点大小的方法会存在浪费的情况,比如下图
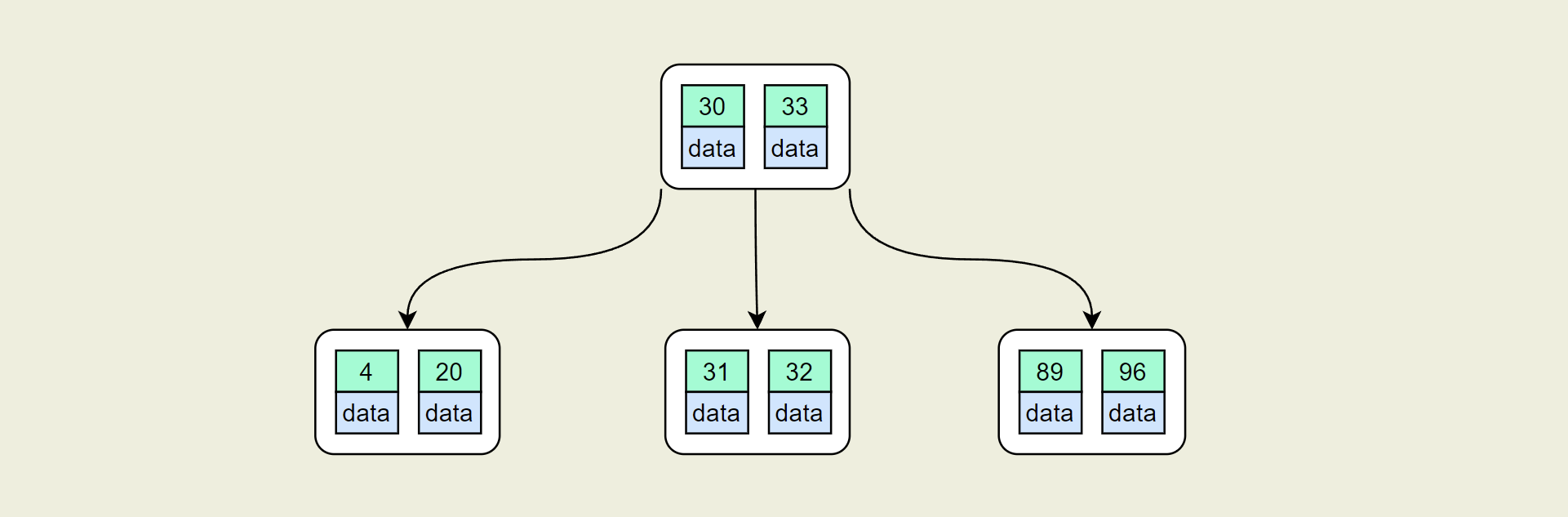
key为31,32所在的结点,已经不可能继续在插入任何值了,因为这个结点的前序key是30,后继key是33,所有整数值都用完了。所以如果记录先按key的大小排好序, 再插入到B树中,结点的使用率就会很低。
B树的删除操作
B树的删除操作按照如下几个步骤:
-
如果待删除的key位于非叶子结点上,则用后继key(右子树中最小的key)覆盖待删除的key,然后在后继key所在的节点S中删除该后继key。这个后继key一定是在叶子节点上的。执行第2步
-
判断S结点key个数是否大于等于
ceil(M/2)-1,结束删除操作,否则执行第3步。 -
如果S结点的左(或者右)兄弟结点key个数大于
ceil(M/2)-1,则父结点中的key下移到该结点,兄弟结点中的一个key上移,删除操作结束。否则将父结点中的key下移与当前结点及它的任一兄弟结点中的key合并,形成一个新的结点。原父结点中的key的两个孩子指针就变成了一个孩子指针,指向这个新结点。然后当前结点的指针指向父结点,此时父节点少了一个key,首先看这个父节点是否是根节点,是的话结束删除操作。否则需要判断是否满足B树的节点个数限制,递归重复第2步。 -
如果待删除的key位于叶子结点上,则直接执行第2步。
上面的步骤没有包含一种特殊情况,需要单独列出:
- B树只有一个根节点,此时删除key没有任何限制
下面同样5阶B树为例:删除44
- 首先找到后继节点S [60,75]
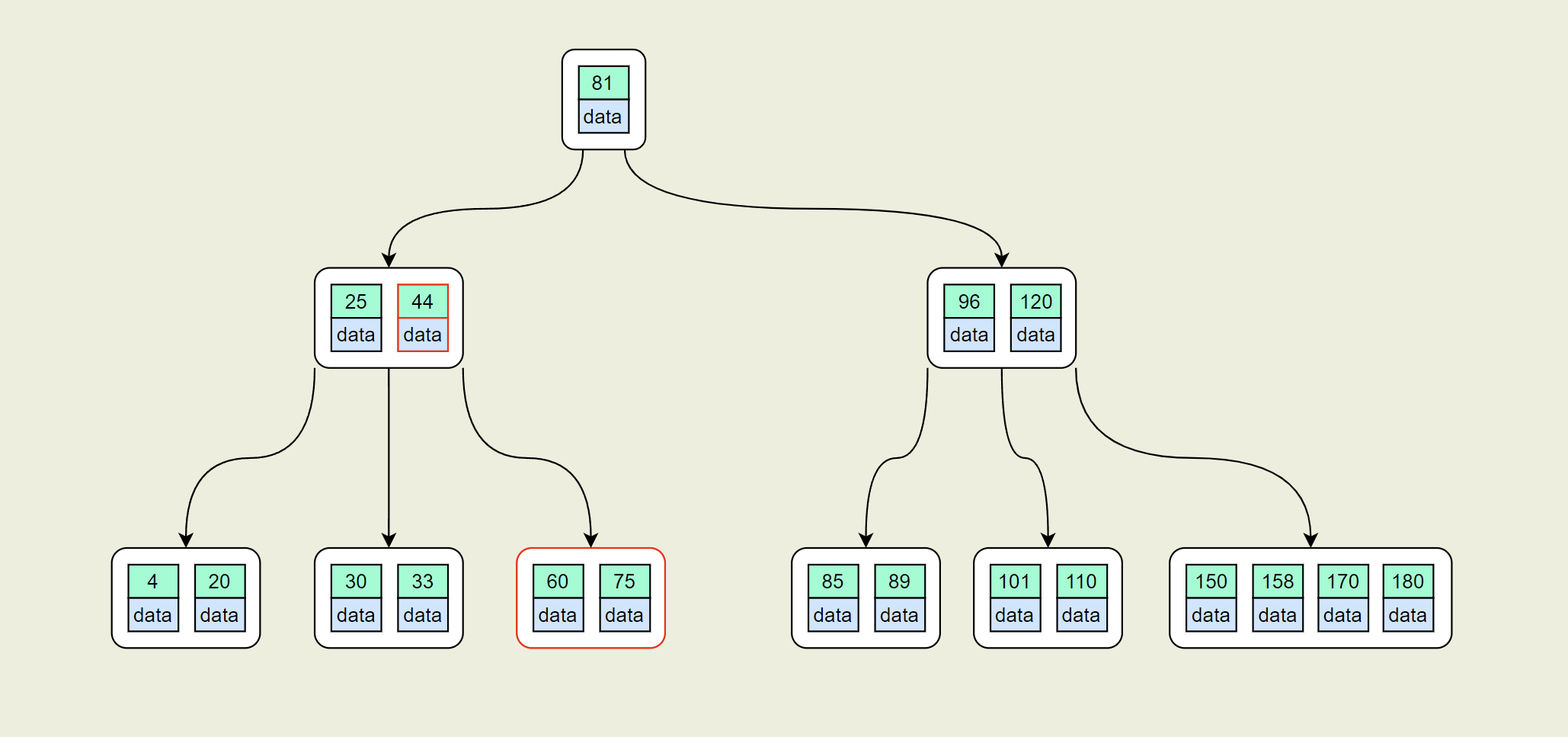
- 使用最小的60替换44,并删除60
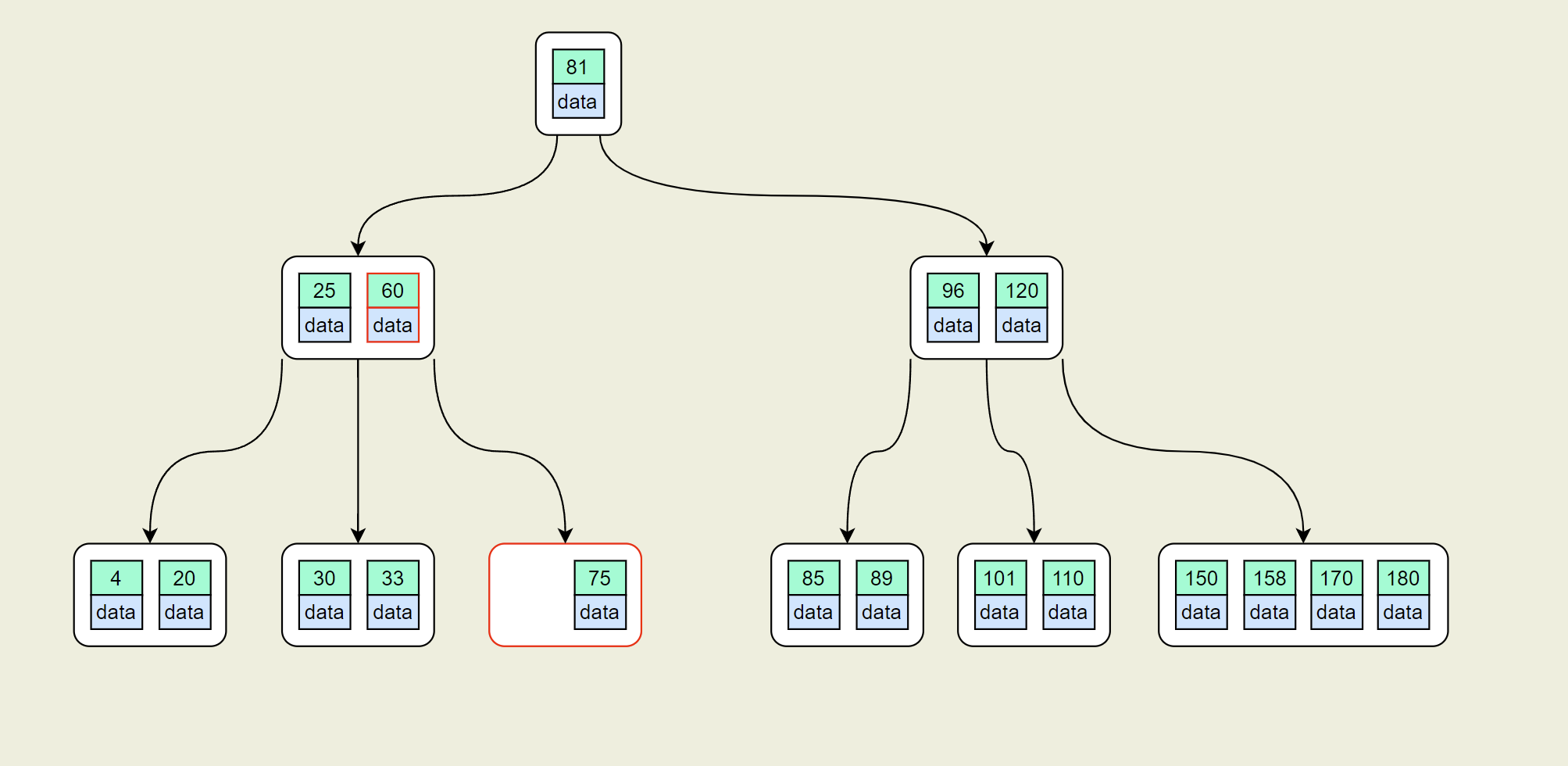
- 此时S节点key数目为1,不满足最低的2个。继续查找它的兄弟节点,发现左兄弟节点[30,33] 不能借。只能合并兄弟节点
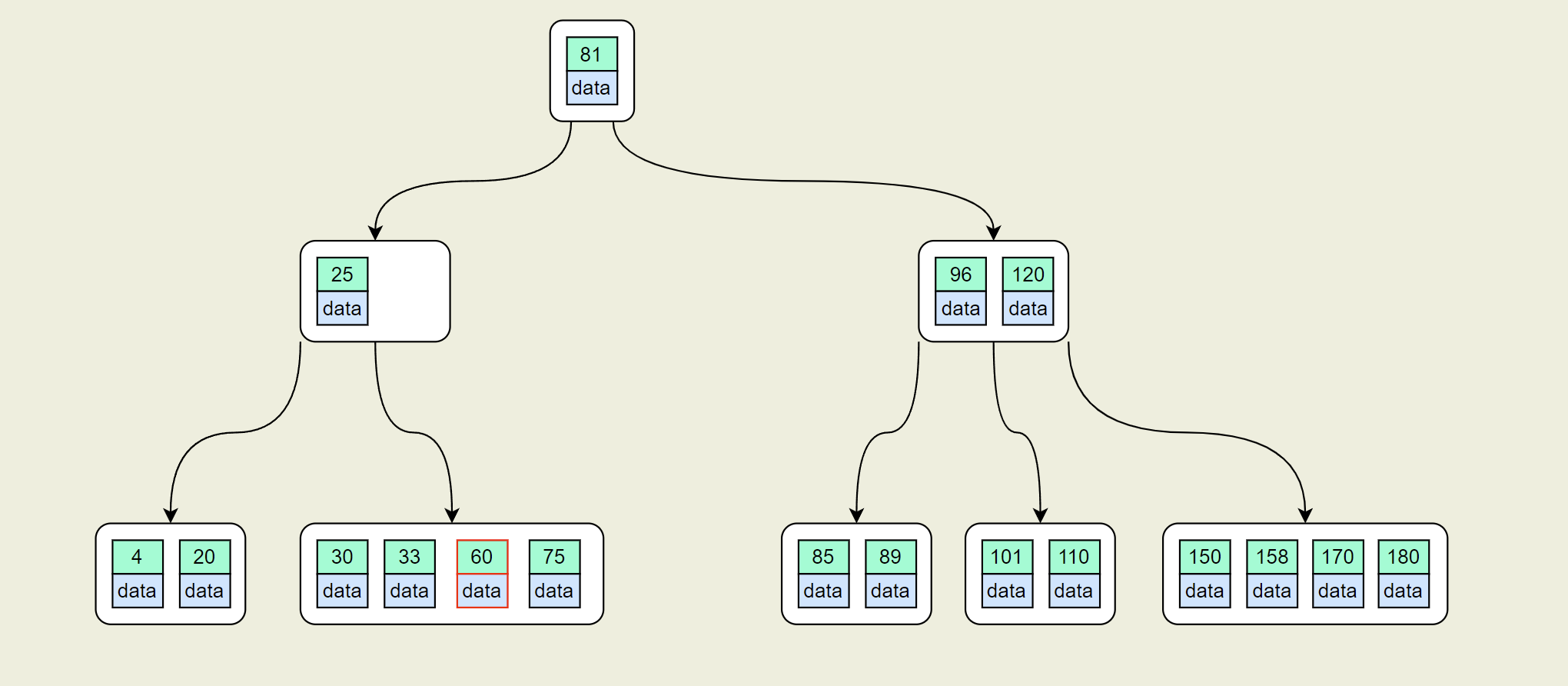
- 此时[25]节点key数目为1,不满足最低的2个。继续查找它的兄弟节点,发现右兄弟节点[96,120] 不能借。只能合并兄弟节点
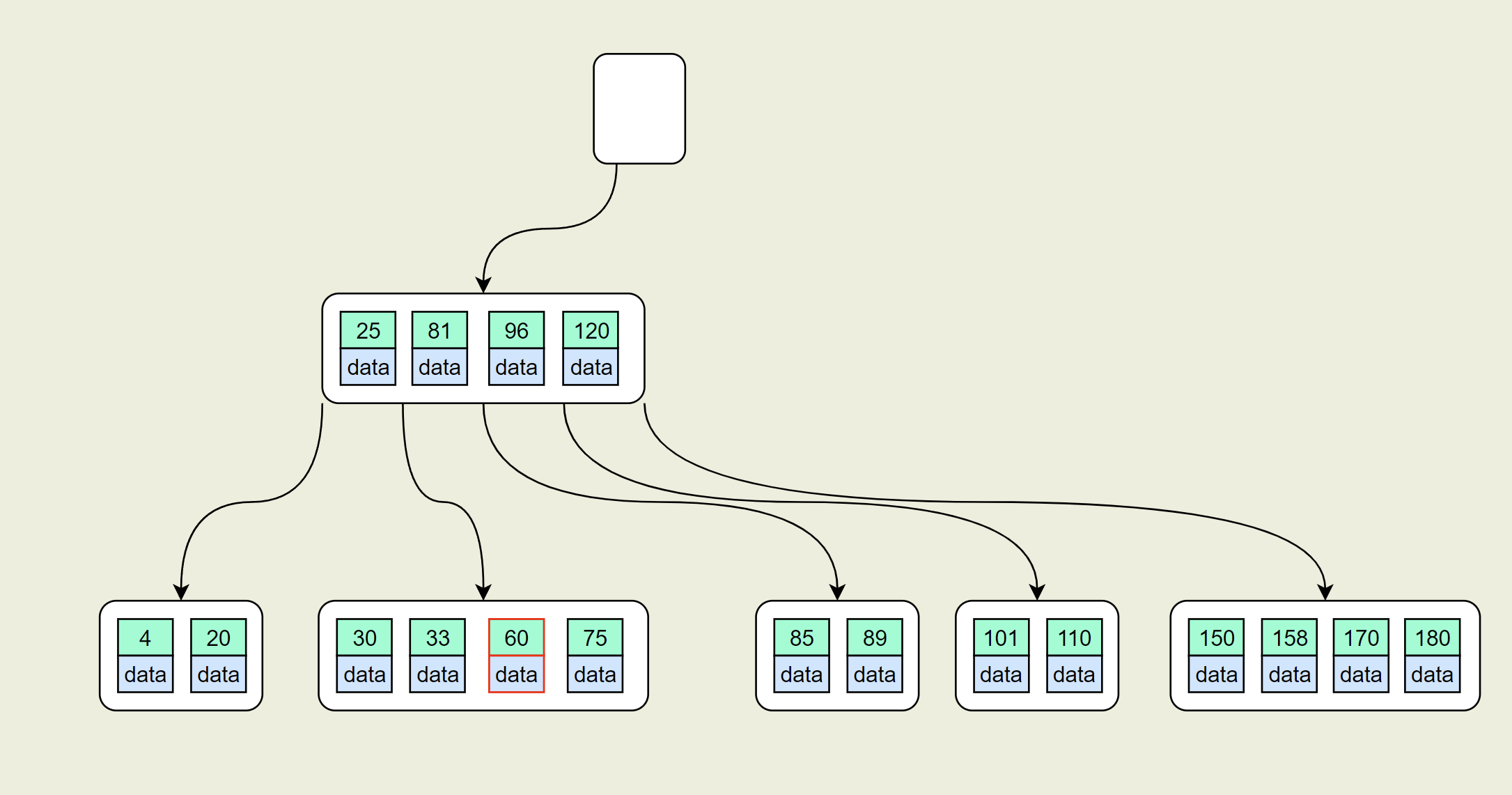
- 移除没有key的根节点,最终得到
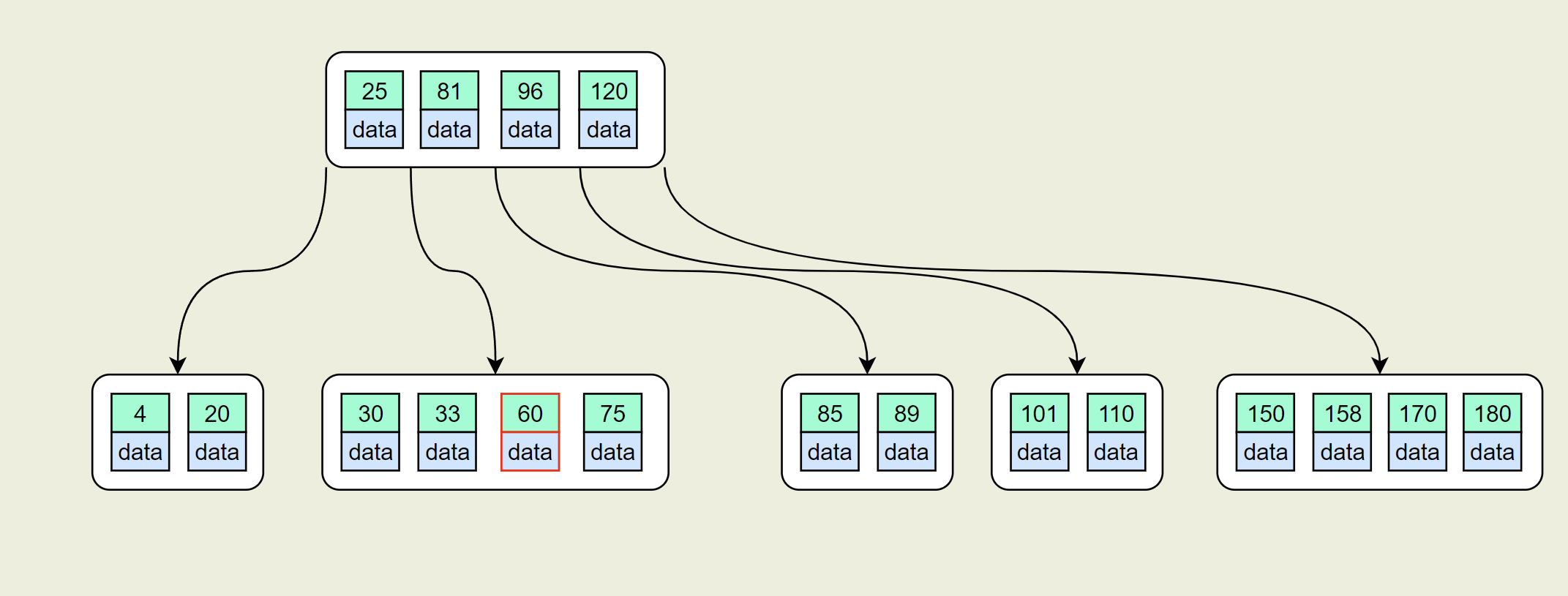
上面的例子没有体现出当兄弟节点可以借的情况。当兄弟接口可以借时,不要忘记将被借节点中相应的子节点也移动到目标节点的子节点中。
下面是一个简化的go实现,忽略了Data,只使用key来表示一个关键字。
// Package btree github.com/leolu9527/algorithm/btree
package btree
import (
"math"
"sort"
)
type position int
const (
left = position(-1)
none = position(0)
right = position(+1)
)
type Int int64
func (a Int) Less(b Item) bool {
return a < b.(Int)
}
type Item interface {
Less(than Item) bool
}
// NewBtree 创建m阶B树
func NewBtree(m int) *BTree {
if m < 3 {
panic("m >= 3")
}
var bt = &BTree{}
bt.root = createNode(bt.m)
bt.m = m
bt.minItems = int(math.Ceil(float64(m)/2) - 1)
bt.maxItems = m - 1
return bt
}
func createNode(m int) *node {
var node = &node{}
node.items = make([]Item, m+1)
node.items = node.items[0:0]
return node
}
type items []Item
func (s items) find(key Item) (index int, exist bool) {
i := sort.Search(len(s), func(i int) bool {
return key.Less(s[i])
})
if i > 0 && !s[i-1].Less(key) {
return i - 1, true
}
return i, false
}
type children []*node
type node struct {
items items //关键字
children children //叶子节点
parent *node
}
// 获取key
func (n *node) get(key Item) Item {
i, found := n.items.find(key)
if found {
return n.items[i]
} else if len(n.children) > 0 {
return n.children[i].get(key)
}
return nil
}
// 获取key
func (n *node) getKey(key Item) (*node, int) {
i, found := n.items.find(key)
if found {
return n, i
} else if len(n.children) > 0 {
return n.children[i].getKey(key)
}
return nil, 0
}
func (n *node) insert(bt *BTree, key Item) {
i := sort.Search(len(n.items), func(i int) bool {
return key.Less(n.items[i])
})
newItems := append(n.items[0:i], append(items{key}, n.items[i:]...)...)
n.items = newItems
bt.split(n)
}
// 获取key节点的左右子节点
func (n *node) getChildNodes(index int) (l, r *node) {
if len(n.children) == 0 {
return nil, nil
}
return n.children[index], n.children[index+1]
}
// 获取key节点的左右兄弟节点
func (n *node) getBrotherNodes() (l, r *node) {
if n.parent == nil {
return nil, nil
}
index := 0
for i, pn := range n.parent.children {
if pn == n {
index = i
break
}
}
if index == 0 {
return nil, n.parent.children[1]
} else {
if len(n.parent.children) == index+1 {
return n.parent.children[index-1], nil
} else {
return n.parent.children[index-1], n.parent.children[index+1]
}
}
}
// 获取后继节点
func (n *node) getSuccessorNode(index int) *node {
ln := n.children[index+1]
if len(ln.children) == 0 {
return ln
}
for nod := ln.children[0]; nod != nil; ln = ln.children[0] {
}
return ln
}
func (n *node) delete(index int) Item {
key := n.items[index]
if index == 0 {
n.items = append(items{}, n.items[1:]...)
} else {
n.items = append(n.items[0:index], n.items[index+1:]...)
}
return key
}
// 移除一个子节点
//TODO 下标越界可能
func (n *node) deleteChild(index int) {
if index == 0 {
n.children = append(children{}, n.children[1:]...)
} else {
n.children = append(n.children[0:index], n.children[index+1:]...)
}
}
//前后插入一个子节点
func (n *node) addChild(move *node, p position) {
if p == left {
n.children = append(children{move}, n.children...)
}
if p == right {
n.children = append(n.children, move)
}
move.parent = n
}
// 获取node在父节点中的index
func (n *node) getIndexInParent() int {
if n.parent == nil {
panic("n is root node")
}
index := 0
for i, pn := range n.parent.children {
if pn == n {
index = i
break
}
}
return index
}
type BTree struct {
root *node
m int //阶
minItems int //除根节点外单个节点最少包含的元素数量
maxItems int //单个节点最多包含的元素数量
}
// Get 查找
func (bt *BTree) Get(key Item) Item {
return bt.root.get(key)
}
// InsertMultiple 批量插入
func (bt *BTree) InsertMultiple(keys []int) {
for _, v := range keys {
bt.Insert(Int(v))
}
}
// Insert 插入数据
func (bt *BTree) Insert(key Item) {
if bt.Get(key) != nil {
return
}
node := getRightNode(bt.root, key)
node.insert(bt, key)
}
// Delete 删除key
// 借不到 合
func (bt *BTree) Delete(key Item) {
n, i := bt.root.getKey(key)
if n == nil {
return
}
if len(n.children) == 0 && n.parent == nil { //只有一个根节点
n.delete(i)
return
}
if len(n.children) == 0 && n.parent != nil && len(n.items) > bt.minItems { //叶子节点 & 节点数量充足
n.delete(i)
return
}
if len(n.children) == 0 && n.parent != nil && len(n.items) <= bt.minItems { //叶子节点、节点不足
n.delete(i)
bt.reBalance(n)
return
}
if len(n.children) != 0 { // 非叶子节点
sn := n.getSuccessorNode(i)
n.items[i] = sn.items[0] //后继替换
sn.delete(0) //后继key删除
bt.reBalance(sn)
return
}
}
//合并两个节点
func (bt *BTree) mergeNodes(l, r *node) {
ix := l.getIndexInParent()
k := l.parent.delete(ix)
rChildren := r.children
l.items = append(l.items, k)
l.items = append(l.items, r.items...)
l.parent.deleteChild(ix + 1)
// 右子分支合并到左分支中
if len(l.children) > 0 {
for _, v := range rChildren {
v.parent = l
}
l.children = append(l.children, rChildren...)
}
if l.parent.parent == nil && len(l.parent.items) == 0 { //根节点
l.parent.children = make(children, 0)
l.parent = nil
bt.root = l
} else {
//递归向根验证
bt.reBalance(l.parent)
}
}
//再平衡
func (bt *BTree) reBalance(n *node) {
if n.parent == nil {
return
} //根节点
if len(n.items) >= bt.minItems {
return
}
//判断兄弟节点是否可借
var bn *node = nil
p := none
l, r := n.getBrotherNodes()
if l != nil && len(l.items) > bt.minItems {
bn = l
p = left
}
if bn == nil && r != nil && len(r.items) > bt.minItems {
bn = r
p = right
}
if bn != nil { //可借
var key, pk Item
ix := bn.getIndexInParent()
if p == left {
key = bn.delete(len(bn.items) - 1)
pk = bn.parent.items[ix]
bn.parent.items[ix] = key
n.items = append(items{pk}, n.items...)
//借完需要处理子节点的归属问题
if len(bn.children) > 0 {
moveChild := bn.children[len(bn.children)-1]
bn.deleteChild(len(bn.children) - 1)
n.addChild(moveChild, left)
}
} else {
key = bn.delete(0)
pk = bn.parent.items[ix-1]
bn.parent.items[ix-1] = key
n.items = append(n.items, pk)
//借完需要处理子节点的归属问题
if len(bn.children) > 0 {
moveChild := bn.children[0]
bn.deleteChild(0)
n.addChild(moveChild, right)
}
}
} else { //不可借
if l != nil {
bt.mergeNodes(l, n)
} else {
bt.mergeNodes(n, r)
}
}
}
// 插入拆分
func (bt *BTree) split(n *node) {
if len(n.items) <= bt.maxItems {
return
}
middle := bt.m / 2
l := make(items, middle)
r := make(items, middle)
copy(l, n.items[:middle])
copy(r, n.items[middle+1:])
middleItem := n.items[middle]
n.items = l
//右节点
rNode := createNode(bt.m)
rNode.items = r
if n.parent != nil { //有父节点
i := n.getIndexInParent()
if i == 0 {
n.parent.items = append(items{middleItem}, n.parent.items[:]...)
n.parent.children = append(n.parent.children[0:1], append(children{rNode}, n.parent.children[1:]...)...)
} else {
n.parent.items = append(n.parent.items[0:i], append(items{middleItem}, n.parent.items[i:]...)...)
n.parent.children = append(n.parent.children[0:i+1], append(children{rNode}, n.parent.children[i+1:]...)...)
}
rNode.parent = n.parent
//递归处理父节点
bt.split(n.parent)
} else { //没有父节点
newRoot := createNode(bt.m)
newRoot.items = append(newRoot.items, middleItem)
newRoot.children = append(newRoot.children, n, rNode)
n.parent = newRoot
bt.root = newRoot
rNode.parent = bt.root
if len(n.children) > 0 { //处理被拆分节点的子节点
rChildren := make(children, bt.m-middle)
copy(rChildren, n.children[middle+1:])
n.children = n.children[0 : middle+1]
rNode.children = rChildren
for _, v := range rNode.children {
v.parent = rNode
}
}
}
}
// 获取待插入的叶子节点
func getRightNode(root *node, key Item) *node {
//根节点
if len(root.children) == 0 {
return root
}
for index, item := range root.items {
if key.Less(item) {
return getRightNode(root.children[index], key)
}
}
return getRightNode(root.children[len(root.items)], key)
}
example_test.go
package btree_test
import (
"fmt"
"github.com/leolu9527/algorithm/btree"
)
func Example() {
bt := btree.NewBtree(5)
bt.Insert(btree.Int(4))
bt.InsertMultiple([]int{20, 44, 89, 96, 25, 30, 33, 60, 75, 81, 85, 110, 120, 101, 150, 158, 130, 135, 138})
fmt.Println(bt.Delete(btree.Int(44)))
fmt.Println(bt.Delete(btree.Int(138)))
fmt.Println(bt.Delete(btree.Int(99)))
// Output:
// true
// true
// false
}
附录
代码:https://github.com/leolu9527/go-algorithms/tree/main/btree
References
Last modified on 2022-05-31
Comments Disabled.